E. Maximum Subsequence

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an array a consisting of n integers, and additionally an integer m. You have to choose some sequence of indicesb1, b2, ..., bk (1 ≤ b1 < b2 < ... < bk ≤ n) in such a way that the value of 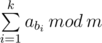 is maximized. Chosen sequence can be empty.

Print the maximum possible value of .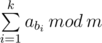

Input

The first line contains two integers n and m (1 ≤ n ≤ 35, 1 ≤ m ≤ 109).

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109).

Output

Print the maximum possible value of .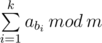

Examples

input

Copy

4 4 5 2 4 1

output

Copy

3

input

Copy

3 20 199 41 299

output

Copy

19

Note

In the first example you can choose a sequence b = {1, 2}, so the sum 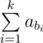 is equal to 7 (and that's 3 after taking it modulo 4).

In the second example you can choose a sequence b = {3}.

/*折半搜索，把取模后的和存起来 双指针统计答案 */#include
      
       #define N 300000using namespace std;int a[N],p[N],q[N];int k,t,ans,n,m,b,dep,flag;inline int max(int x,int y){
    return x>y? x:y;}inline int read(){    int x=0,f=1;char c=getchar();    while(c>'9'||c<'0'){
    if(c=='-')f=-1;c=getchar();}    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}    return x*f;}void dfs(int now,int sum){    if(now==dep)    {        if(!flag)        {            p[++k]=sum,p[++k]=(sum+a[b])%m;return;        }        else        {            q[++t]=sum,q[++t]=(sum+a[n])%m;            return ;        }    }    dfs(now+1,sum);    dfs(now+1,(sum+a[now])%m);}int main(){    n=read(),m=read(),b=n>>1;dep=b;    for(int i=1; i<=n; ++i) a[i]=read();    if(n==1) printf("%d",a[1]%m),exit(0);    flag=0;dfs(1,0);    dep=n;flag=1;dfs(b+1,0);    int L=0,R=t;    sort(p+1,p+k+1);sort(q+1,q+t+1);    while(L<=k)    {        while(p[L]+q[R]>=m) --R;        ans=max(ans,p[L]+q[R]),++L;    }    ans=max(ans,p[k]+q[t]-m);    printf("%d",ans);    return 0;}